Chapter 1: What is Fractal Management Theory
What is Fractal Management?
Fractal Management is a way of storytelling and it is a methodology for observing and changing scalability attunement in organizations. The Organizaiton is inrelation to its environments. Fractal storytelling is a way people in organization attune to the sociomateriality (see chapter 2) of fractal space-time-mattering. We can zoom in and zoom out in our storied observations of the relationship of organization and environments.
The word fractal in Latin is fractus and means to be broken, jagged, uneven, with repeating shapes of self-sameness or irregualr curves across different scales. Latin verb frangere means to break or create irregular fractments. We will relate fractal (fractus and frangere) to attunement. People in organizaitons are somehow attuned to fractality.
First, starting definitions: "A fractal is most generally defined as a structure which displays increasingly more detail as one zooms into it" (Vrobel, 2011: 18). Benoit Mandelbrot (1975) coined the term fractals. Mandelbrot’s definition of fractals: “irregular and/or fragmented at all scales” (Nottalle, 2011: 44).
Fractal Management, therefore is defined here as an attunement to repeating and non-repeating sameness and irregularness in managing and organizaing the sociomateriality of organizations. Sociomateriality (see chapter 2) is how the social and the materiality are interactive (or intra-active), and interpenetrating.
What are Fractals in Management Science?
A breif history is necessary before answering this quesiton.
There have been many contributions to fractal geometry:
"According to legend, the Greek Philosopher Pythagoras [born 569 BC - died between 500-475 BC] discovered the concept of harmony when he began his studies of proportion while listening to the different sounds given off when the blacksmith’s hammers hit their anvils" (Greek Golden Ratio, bracketed addition, ours). This is an example of what we mean by attunement. The hammers (by weight) and anvils (by wieght) give off different sounds, to which the attuned body, can hear, and resonate. "Pythagoras believed that beauty was associated with the ratio of small integers" (IBID.). Our friend and colleauge Gerri McCulloh is writing her dissertaiton on Pythagoras and his contribution to materialism rhetoric.
Phidias (500 BC – 432 BC), a Greek sculptor and mathematician, studied phi and applied it to the design of sculptures for the Parthenon. (Golden Number, online). An Plato (circa 428 BC – 347 BC) said it was the most fundamental of all relationships.
"Euclid ( 330- 275 B.C. ) proposed lines with infinite lengths to illustrate the concept of parallel lines, there he also used self-similar triangles to show the congruency of triangles..." (Fractal Explorer, online)
"Archimedes (287-212 B.C.) used spirals to illustrate repeating transformations...." (Fractal Explorer, online) E.g. the Archimedes sprial, whorls expand at a constant scale (such as in a bolt thread pattern).
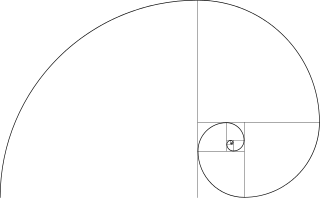
Italian matematician Leonardo Bonacci Fibonacci (c. 1170 – c. 1250) introduced the Fibonacci number sequence, where each next number is the sum of the previous two: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 … This can be used to create the Fibonacci Spiral:
Figure 1; Fibonacci spiral (source, no permission needed).
This is also known as a Logrithmic Spiral. And if you take the ratio of the two numbers added together in the Fibonacci series, it approximates the Greek Golden Ratio.
"Mathematician Jacob Bernoulli (1654-1705) expanded this idea to show that some spirals could be drawn with an infinite length, of which the logarithmic spiral is the most famous" (Fractal Explorer, online) E.g. the Logrithmic spiral, whorls expand at ever increasing sale (such as spiroidal shells: snail shell, conch shell, etc.).
"Felix Hausdorff (1868-1942) and Abram Besicovitch(1891-1970) revolutionized mathematics by proposing dimensions with non-integer values." This served to expand the fractal dimensionality" (Fractal Explorer, online).
"Lewis Fry Richardson (1881-1953), an English meteorologist, pioneered a process for calculating dimensions with varied measurements." His work is famous for oastline calculaitons, and for spiral fractals. "It was Richardson's work that prompted Mandelbrot and others to ask the now famous question 'How Long is the Coast of Britain ?'" (Fractal Explorer, online).
" Big whorls have little whorls,
Which feed on their velocity;
And little whorls have lesser whorls
And so on to viscosity
(in a molecular sense). "
- Lewis Fry Richardson
Here we apply fractals to management science. Organiztaions and their environments form fractal relationships of irregular and/or fragmented scales.

Figure 1 - Broccoli Romanesco approximates fractal structures and fractal-spiral cones (image source)
"The Broccoli Romanesco exhibits fractal structure in its perimeter, planar and volumetric dimensions" (Fractal Explorer, online). However, keep in mind, this is an approximation to the fractal geometry, since the fractal patterns only occurs at a few levels of magnification. There is a jaggedness-appearance in the irregular boundary (perimeter dimension). We can do crosssections to get at the planar fractal dimension.
How is this related to Fractal Storytelling?
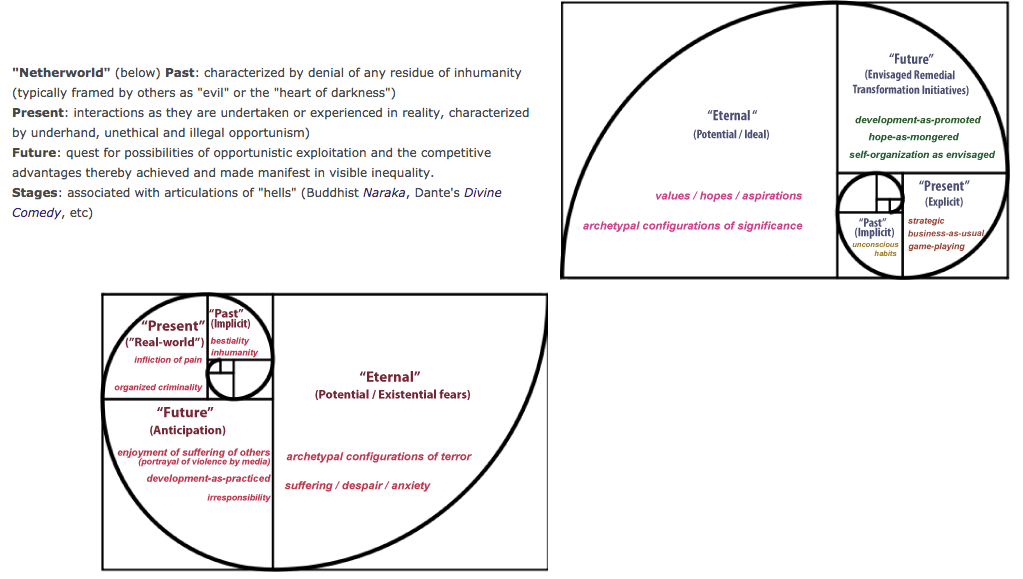
Figure 2: Mirroring Upper and Lower World in Fibonacci Double Spiral (source)
The above image may be "distorted" to illustrate contrasting attitudes to netherworld/upperworld, or even restorying global governance, by skewing, distorting, or resizing the spiral mirror images. Keep in mind that the spiral image is not idientical to the fractal patterns of globalizaiton or other patterns of organizing.
In sum, fractal management theory is defined here as the way people in organizations are attuned to fractal dimensions and enact fractal storytelling. Fractal storytelling (or fractal story) is not the same as what the fractal mathematics define as fractal perimeter, plane,volume, self-similar or irregularity scalability.
Fractal Management
Human systems self-organize. The exact outcomes are tough to predict, but the kinds of patterns seem to he a signature of how the human race behaves. We coalesce around a common goal or belief, grow in harmony, then eventually create in and out groups, then cling to an illusion of control when the fighting gets bad enough to threaten those who have managed to place themselves atop the hierarchy. Change then comes from the bottom up, sometimes violently, and the cycle begins again. Numerous works of fiction have depicted this cycle, most notably George Orwell’s Animal Farm.
This occurs not only in the realm of nation building, but in other places as well. Think about the patterns of group behavior that we see in organizations, households, and even on an individual level. Ruby Payne’s work, Bridges Out of Poverty demonstrates these sorts of patterned behavior in the context of the generationally poor.
I seems to be a central part of the aggregate human condition. We need to establish some sense of order and control as we begin cooperating for mutual gain.
What is the basic fractal unit of human organization? --- see that book about fractal orgs & critique sucky description then propose our own
How do we manage when faced with the idea that organizations will behave in this manner? What is the best way to navigate?
It has been shown that adaptation is pivotal to sustainability in organizations and individuals. It has been identified as a core competency in organizational strategy (Worley, Hitchin, & Ross, 1996).
To foster adaptation it is useful to understand not only the patterns we see within a given context, but also to understand the core principles that foster the repetition of these patterns. One way to get at this is to ask successful people where they see scalable, self-similar repetition and go from there. In a study of eleven nonprofit executives, we found that using a content-agnostic interview protocol that simply asked where the subjects saw fractal patterns in their work lives yielded insights into the operating principles behind their success (Wakefield, 2012). The same approach has been used in other contexts to further demonstrate the methodology (Henderson & Deporres, 2014; Wakefield, Boje, & Lane, 2013).
The practical application of these learnings comes in the form of an action research model. The Fractal Action Research Model (FARM) originally consisted of X steps.
Here is an example of three zoom-zones of self-same fractals.
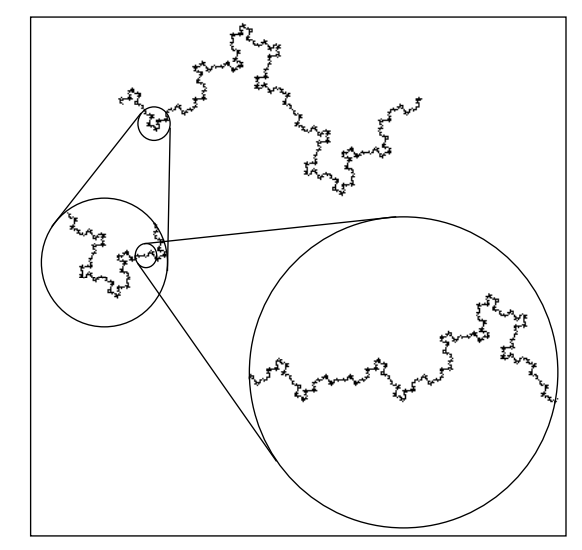
Figure 4 - Selfsame Fractal Zoom-Zones (source Nottale, 2011: 41)
The above figure from Nottale (2011: 41) shows structure at several zoom-scales at different levels of observation. Fractals show structures at all these scales.
But does the manager see them all? A manager can get stuck in one of these zoom-scale understanding a constrited or very dilated one, and be attuned to only that one scalability. With training and experience, the manager can learn to be attuned to alternative zoom scales.
Fractality with self-similarity only characterizes some and not all fractals.
Fractal-Scale-Dependence The research question becomes, to what extent are managers attuned to fractal scalability? Managers, we assume, have developed scale-dependence. This means managing an awareness and actioin orientation attuned to a fractal zoom-scale, for example, with the very local Situation of the organization. The zoom-zones could also be more micro, from the quantum particle/wave to higher scalability.
However, another manager may be attuned to headquarters or to a particular global market. Another could be attuned to the quantum scale. This scale-dependence choice-making by a manager selecting either local, or quantum, or anincreasingly global, even transcendent, understanding of space of organization-and-environment has communicaiton and actual performance consequences.
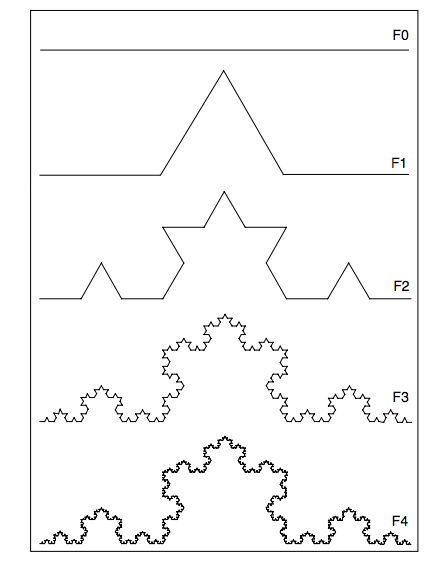
Figure 5 - Koch's Iterative Self-Similar Fractal Curve (Source: Nottale, 2011: 42)
It is discrete similarity, since at each zoom level, the observer observe the same self-similar pattern, with different levels of detail (especially at F2 to F4). A manager at F0 does not have any attunement to finer grained differences. That manager produces a linear observation, when finer attunements are potentially discernable at different scalability. F4 and F3 show smaller structures along the curve than F2 and F1.
Spatial Fractal Resolutions Fractals that are self-similar show structures at all zoom-scales (observed/measured at different spatial resolutions). The power law:
"Therefore, the power law divergence of self-similar fractals is only a very particular case, and several other modes of divergence are possible, including slower divergences of the logarithmic type or fasterdivergences of the exponential type" (IBID.: p. 57)
Temporal Fractal Resolutions Fractals are not just topological. There can also be temporal fractals. The fractal curve can manifest in-time, at various speeds, and our observation of time fractals needs to have a measurement method that is attuned to the fractal curve's temporality.
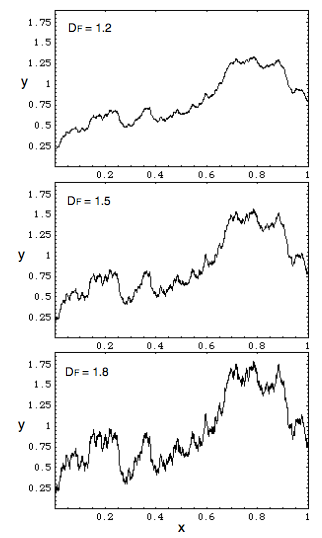
Figure 6 - Temporal Fractal Resolution (Source Nottale, 2011: 52)
In this figure, the plot are over time, and depending on the observation resolution, there is less or more assessment of finer structures. All three resolutions give some sense of the trendline.
In other words, there is among managers, scale-divergence, in focusining on scales of finer or grosser structures, and dependence upon topological (spatial) or temporality differentiations. This fractality scale-divergence has consequences for how managers are understanding strategy, history, operations, and ecology. this resolution orientation of managers' attunment is something worked out in specializaiton and experience.
Scale Transformations
How are scale transformations happening in organizations? We assume that people in organizaitons become scale-dependent, and therefore attuned to different fractal-resolution patterns. The classic view is those at the top of the hierachy of an organization have a wider field of vision, but are not sensitive to the finer-structures, as are those in the technological core, or on the ground, in the bottom of the hierarchy. Managers, then, are in-between, making out both the wider and narrow resolutions of fractal structures.
Fractal space-time management observations can get into a rut. By improving resolution relative to the task at hand, the strategic horizon can shift.
"Wavelets are now widely used for data analysis of fractal, scale dependent and hierarchically organized phenomena, and one needs to construct a theoretical equivalent" (IBID.: p. 63).
Tang (2012) combines Mandelbrot definitions of Fractal (F) into one definition. Mandelbrot's (1983) F-definition is the topological or spatial dimensions of a set of sbustructures. His (1986) definition is that a Fractal (F) is a compound entity composed of subsets of entities, with a global characteristic of self-similarity between the local subsets. Tang (2012: 66) refines the definition: "The global charactistic of the set F is self-similar to the local characteristics of each subset."
The subset entities are infinitely separable, at an infintesimal scale magnification (or resolution, as Nottale, 2011 puts it). Tang, unlike Nottale, is focused on Euclidian understandings of spatial dimensions, usch as Hausdorff. The problem is that the Euclidian understanding of fractals is monological: monotonicity (p. 61), a countable stability, invariant transformations, continuous transformations, and inverse is also assumed to be continuous (p. 63). Tang, however, brings up an interesting problem with the measurement system being used to measure the Fractals (F) and their subset seperations, intervals, and transformations. For example, in the Cantor Dust F, the measurement of a Space (Eo) is to focus on four sub-areas (E1), and then with each one make these into four sub-areas at higher resolution (E2), and so on in (E3), to get at F series.
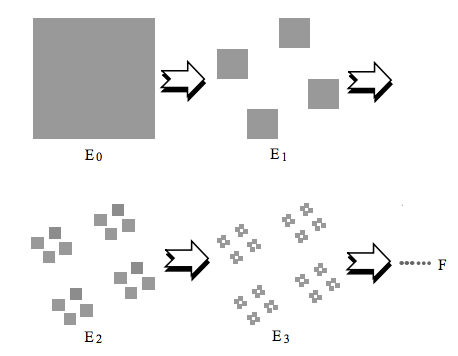
Figure 7 - Cantor Fractal Measurement Example (Tang, 2012: 66)
In fractal observation, an observational apparatus, such as Cantor or Hausforff, that is Euclidian, removes segments of the observed entity, to create intervals, seperations, and so on. These are observation-measurment choices. Here is another example of how the measurement system maps the observed target systemicity, in ways that are reductionistic, selective, and assume Euclidian spatial ontology, in-order-to conduct the (post) positivistic measurement protocol.
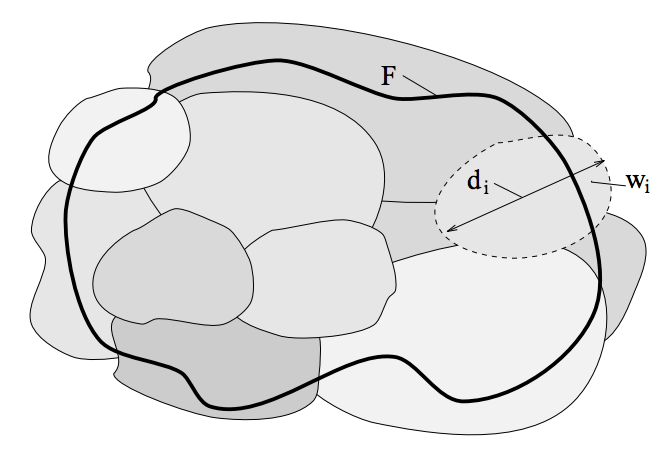
Figure 8 - Box Empirical Estimation of Fractal (Tang, 2012: 70)
The Fractal (F) is measured within the confines of the black circular area, and the diameter (di) of the subset measure (Wi) is taken. "Box dimensions may be thought of as indicatingthe efficiency with which a set may be covered by small sets of equal size, whereas Hausdorff dimension involves coverings by sets of small but perhaps widely varying size" (Tang, 2012: 80). The measurement system has the problem of how to make observations that cover the various subsets of the target systemicity.
Vrobel (2011: 25) raises some challenges to the Box Method of Fractal Observation:
"Another remarkable feature of the Box-Counting Method is that it shifts fractality into the eye of the beholder: Even a non-fractal structure can be looked at through “fractal spectacles” consisting of superimposed grids of various scales. The observer determines the yardstick and hence the measurable extension of any structure, be it spatial or temporal."
Next we look at temporal structures, first in a cruvilinear Fractal sequence, then in nested simultaneous Fractal structures.
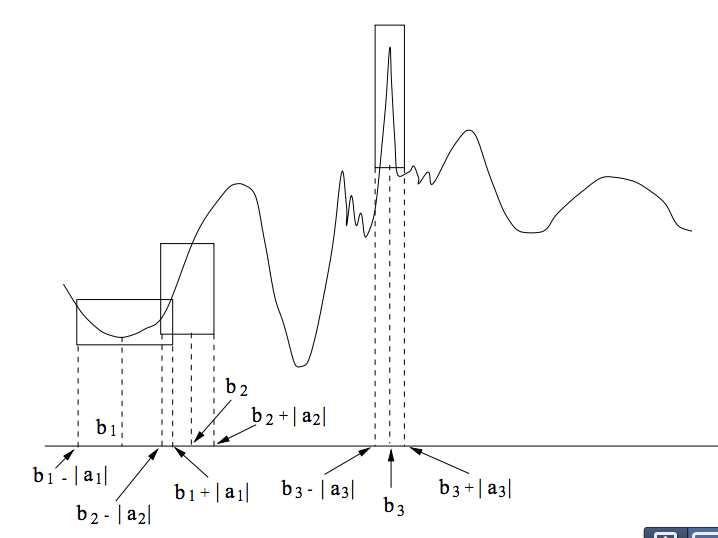
Figure 9 - Measument choices of a Wavelet (Tang, 2012: 97)
There are measurement choices by a measurement-observation-system to observe a target systemicity over temporal horizon. Time intervals are constructed by the measurement-system. The measurement-system can measure local peaks and valleys, upslopes, and downslopes, at various time-intervals of the wavelet's wavelength.
Tang uses the Euclidian measurement algorighms of the Box and the Wavelet methods to assess regions of the text documents. A Fractal (F) pattern can be extracted by the measurement-system by assessing the structural layout of the document (headlines, graphics, sections, etc.) and then mapping the logical structures of the document to approximate 'understanding' (Tang, 2012: 173). For the layout analysis of the text, parts (entities, subsets) are either treated as in-hierarchical relationship to one another, or as non-hierarchic. Part of the documents are broken into successively smaller sup-parts.
In automated text analysis software packages, such as Diction, Leximancer, Crawdad, and Latent Semantic Analysis (LSA), understanding is simulated by either consulting pre-prepared dictionaries (Diction) or developing proximity measures of key words (LSA), of something in-between (Leximancer, Crawdad). This makes analysis between sets of documents possible.
For example, in LSA "A matrix containing word counts per paragraph (rows represent unique words and columns represent each paragraph) is constructed from a large piece of text and a mathematical technique called singular value decomposition (SVD) is used to reduce the number of rows while preserving the similarity structure among columns" (Wiki, LSA). A limitation is LSA cannot capture multiple meanings of a word.Second, LSA assumes with multiple documents, a joint space with an underlying monologic is formed.
"Leximancer is a data-mining tool that can be used to analyse the content of collections of textual documents and to visually display the extracted information" (Leximancer Manual). Leximancer uses proximity calucaltions. It cannot assess actual emotional inflections or nuances: "Affect extraction, which aims at providing an emotional evaluation of the emotional and psychological state of the speaker, is a quite specific form of content analysis that is beyond the scope of this document" (IBID.: p. 27).
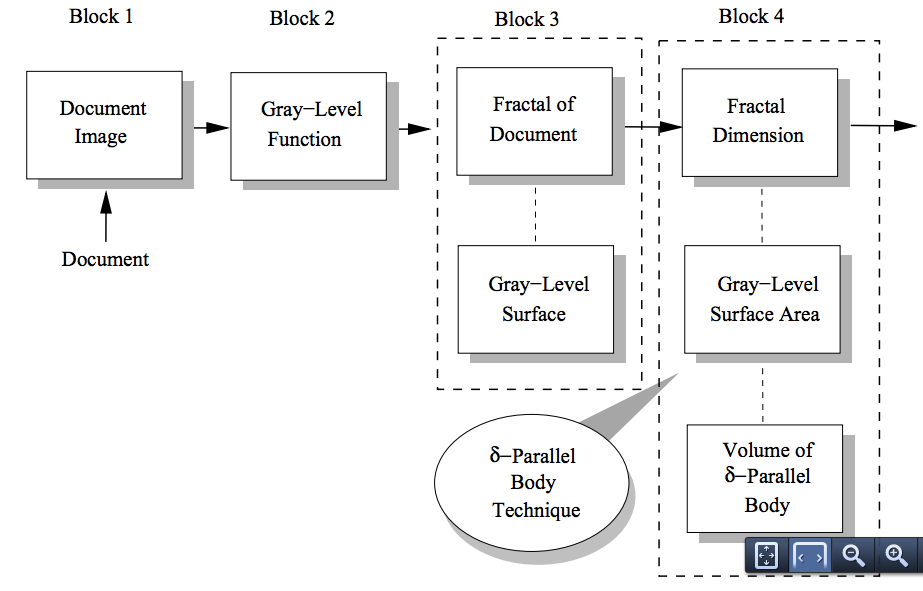
Tang (2012) is attempting to deveal a fractal approach to text analysis, in ways that goes beyond LSA, Leximancer, Crawdad, and Diction. "Fractal is mathematical sets with a high degree of geometricalcomplexity, which can model many classes of time-series data as well as images" (Tang, 2012: 177). Tang's approach is to develop a method to search for a Modified Fractal Signature (MFS) in texts including their images/graphics/photos.
Figure 10 - MFS Method for Document Analysis (Tang, 2012: 180).
Keep in mind Tang is not claiming to actually measure the underlying Fractal direclty. Rather the signature of the Fractal, in its modified form is the being sought.
Wavelet Measures in Text Analysis. "In wavelet-based approach, a document image is decomposed into several sub-images in the frequency domain by wavelet transform, and thereafter, two feature vectors are extracted from these sub-images, namely,
• WED - wavelet energy distribution, and
• WEDP - wavelet energy distribution proportion" (Tang, 2012: 279).
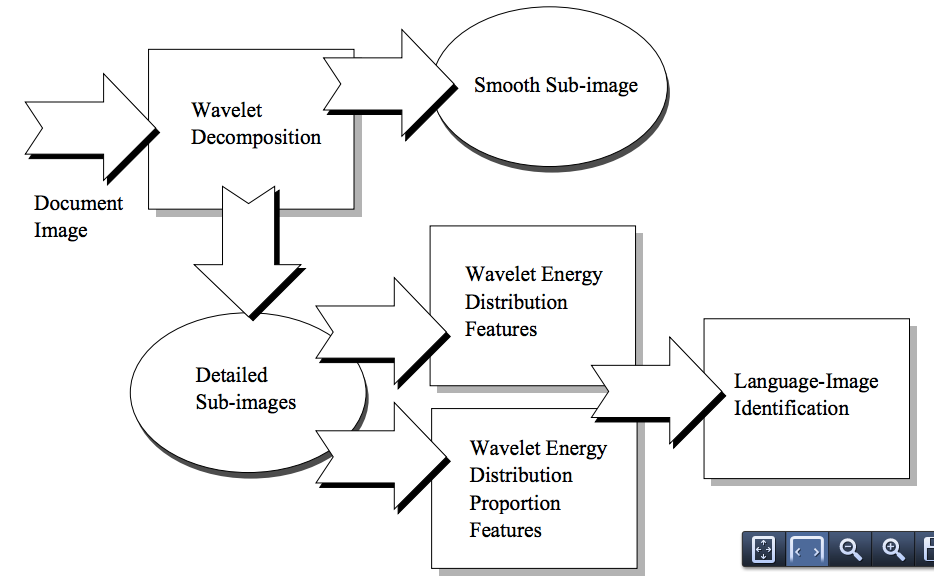
Figure 11 - Wavelet Document Analysis Method (Tang, 2012: 283)
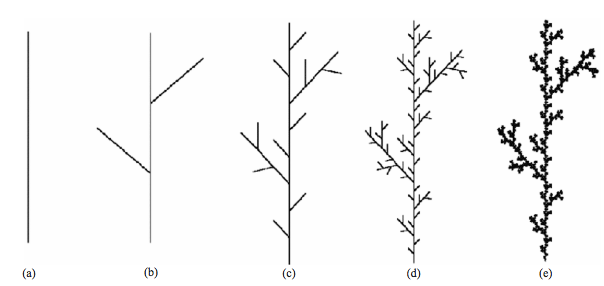
Scott and Gulick (2010) look at plants, how they form F (Fractal) branch structures over time, and at varying scalability resolutions. This approach could help understand how orgnaization structures have replication rules for branching. In a recursion functin, a simple branch rule, gets repeated, over and over again. In plants the recursion function, is the set of instructions that plants follow to branch, when to branch, to flower, and when to flower, etc. Can such a recursion function be applied to understand complex organization Fractal processes?
Figure 12 - Recusion Funciton Rules in Branching at Varying Degress of Resolution (Scott & Gulick, Anne Burnes chapter, 2010: 3)
Far away, at resolution (a), branching is not observable with the measurement-system. However, in (b) two branches, and (c to e) subbranching is discernable by the measurement-system. This allows an assessment of the Fractal Signature by tracing the branching structures, and substructures. This can also be done across an organizational space, and in-time to assess space-time F (Fractal) branching in a recusion function.
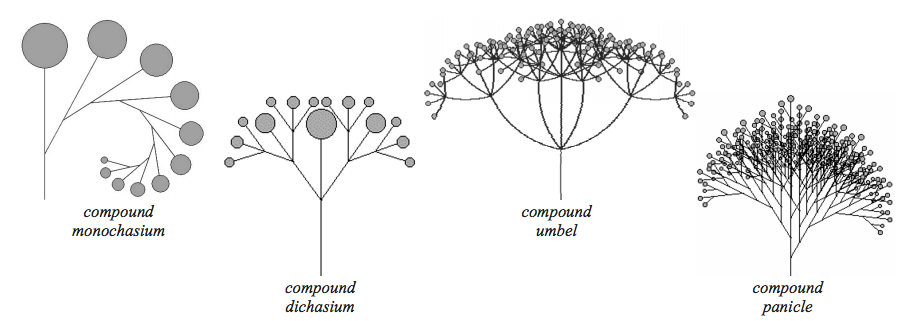
Figure 13 - More complex branching patterns (Scott & Gulick, 2010, Anne Burnes chapter: (p. 12).
This would allow comparison across many organizations in Fractal-space, and across time of a single organization, of Fractal Branching Patterns Temporal Patterns.
"Although the spatial and temporal fractals within human physiology and psychology have been discovered only fairly recently in the wake of chaos theory and theories of complexity, the idea of nested rhythm is not an entirely new one" (Vrobel, 2011: 27).